Quantum Scattering in Confined Geometries

Photo: AG Schmelcher

Introduction

Dimensionality represents a key issue for few- and many-body systems. Depending on whether one, two or all three dimensions are strongly confined the properties and dynamics of interacting bosons show very different features. Modern experiments on ultracold bosonic systems use typically optical or atom chip techniques in order to achieve confining traps in the nanometer regime. For such a tight confinement an indidivual atom atom scattering process feels the confining forces and therefore the free-space scattering properties are severely modified. We focus on two strongly confined dimensions yielding a so-called waveguide with one free dimension left.

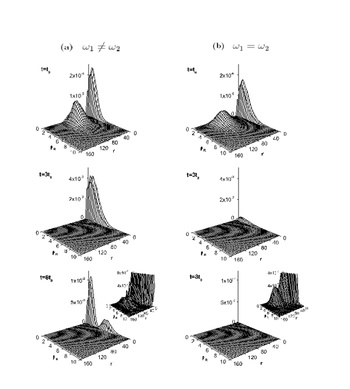
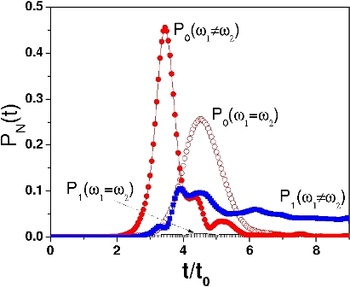
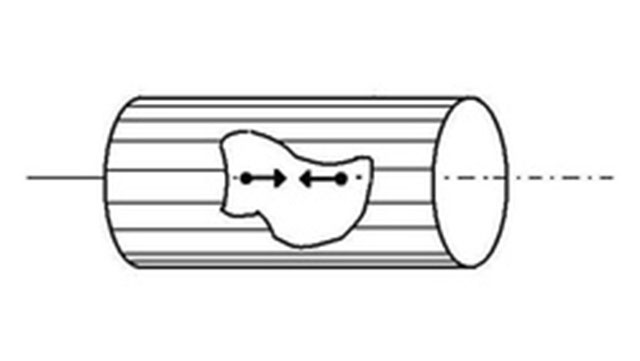
In a seminal work by Olshanii in the late nineties it was shown that the confinement can induce a resonance into the low-energy, ultracold, scattering properties of two bosonic atoms. This resonant behaviour leads to a strong repulsion of the bosons thereby completely suppressing the transmission of the atoms in the waveguide. As a consequence this confinement-induced resonance leads to a so-called Tonks Girardeau gas of hard core interacting bosons which mimic fermionic properties. Changing the confinement allows to tune the effetive interaction strength among the bosons, which is nowadays used in experiments to probe the transition from weakly to strongly correlated many-body systems. Amazingly, the opposite situation, the dual to the confinement-induced resonance, can also happen. If several partial waves take place in the underlying free scattering process, the confinement can lead to a complete suppression of scattering, which is the so-called confinement-induced transparency effect. This effect is due to a destructive interference of the different partial waves participating in the confinement scattering process. In anisotropic and/or anharmonic waveguides the coupling of the center of mass and relative degrees of freedom leads to an energy flow from the external to the internal degrees of freedom. As a consequence molecule formation is possible in a single two atom scattering process. In the ultracold regime one encounters a resonance molecule formation followed by back decay to the continuum thereby establishing a quantum gas of atomic and molecular components in the waveguide.