Quantum and Classical Dynamics of Driven Billiards and Lattices

Introduction

We study the classical and quantum dynamics of (periodically) driven systems. Typical model systems are one-dimensional extended lattices of individually driven barriers or two-dimensional billiards with time-dependent boundaries. Due to the driving, these systems are pushed out of equilibrium. This allows the study of non-equilibrium dynamics such as diffusion in momentum space e.g. Fermi acceleration, or - in the case of spatially extended systems - diffusion in configuration space.

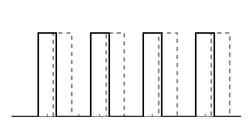
Driven Lattices

The precursor of a driven lattice consisting of harmonically driven barriers is simply a single driven barrier. Already such an apparently simply system possesses a variety of interesting phenomena. For example, there exists stable trapped motion (classical dynamics) for certain parameters, even though the potential of the barrier is always repulsive and the scattering function has a fractal structure. In the quantum case, the transmission through such a time-dependent barrier shows a resonance structure, since there are quasi-bound states in the corresponding effective potential. When considering two such driven barriers next to each other, the transmission of a wave packet through this system does not only depend on its initial energy, but also, among others, on the relative phases of the two barriers, yielding very rich dynamics due to multi-photon processes.

Ratchets

The generalization of a single or a double-barrier system is a driven lattice. Of special interest are the so-called ratchets, where the (periodic) driving force has a zero mean. A remarkable observation is that these systems can nevertheless show directed transport of an ensemble of particles, although there is no net force. The transport is caused by an asymmetry of the underlying phase space. Usually, the asymmetry is caused by applying a bi-harmonic driving law. However, already the transport through such a single bi-harmonically driven barrier favors one direction, resulting in the mentioned directed transport of the extended lattice. We choose a different approach here: Each cell of the extended lattice has its own driving law, which for itself is non-transporting. In the simplest case, we use harmonic driving laws with a phase gradient dependent on the lattice side. The observed directed transport is thus a collective phenomenon, caused by the interplay of the different local driving laws

Billiards

Billiards are a popular toy model in physics, they posses many classical and quantum mechanical properties of complex dynamical systems, even though they are rather simple themselves. Many models of statistical mechanics can be reduced to billiards. For example, one of the simplest billiards, particles inside a rectangular box, is an idealization of the physical situation of nucleons confined inside a nucleus. A renewed interest in billiards has come up in the last years, due to the possibilities of realizing them experimentally, for example by using ultracold atoms confined in a laser potential (matter wave billiards), by using microwave in a (superconducting) cavity or by using mesoscopic quantum dots. Also for the design of directional micro-lasers, billiards are relevant.

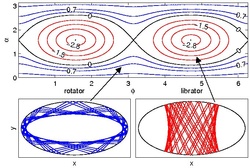
What is a Billiard?

A billiard typically consists of a smooth, closed curve in the two-dimensional plane, the billiard boundary. Point particles inside the billiard propagate ballistically until they hit the boundary. Usually no particle-particle interactions are assumed. Upon collisions with the wall, the particles are reflected elastically, so the billiard boundary is considered to be infinitely heavy and the energy of the particles is conserved. The dynamics of such a system is exclusively determined by the shape of the boundary and can range anywhere from integrable to fully chaotic motion.

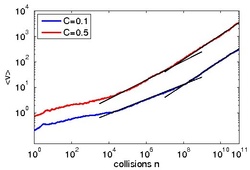
Driven Billiards

Time-dependent billiards are a natural generalization of billiards with static boundaries. By time-dependent, we mean that the boundary of the billiard is driven, i.e. the geometry of the billiard changes in time. As a consequence, particles colliding with the moving boundary can loose or gain momentum, the energy is not conserved anymore. This allows the study of non-equilibrium processes such as Fermi acceleration (FA), which is the unbounded energy gain of particles exposed to driving forces. FA was first proposed in 1949 by Enrico Fermi to explain the high energies of cosmic radiation. He suggested that charged particles repeatedly interact with time-dependent magnetic fields (originating either from shockwaves of supernovae or from magnetized interstellar clouds) in such a way that on average they gain energy. Nowadays, FA is investigated in a variety of systems belonging to different areas of physics, such as astrophysics, plasma physics, atom optics and has even been used for the interpretation of experimental results in atomic physics.

Whereas in one dimension it is clear under which conditions FA will arise, in two dimensions the situation is much more complicated, since the phase space is now four dimensional. The driven elliptical billiard exhibits FA even when using a harmonic driving law (in 1D, stochastic driving laws are necessary to obtain FA). The corresponding transport process in momentum space shows a surprising crossover from sub- to normal diffusion. This crossover is not parameter induced, but rather occurs dynamically in the evolution of the ensemble. The stickiness properties, which eventually determine the diffusion, are intimately connected with the change in the composition of the phase space with respect to velocity. In the course of the evolution, the accelerating ensemble thus explores regions of varying stickiness, leading to the mentioned crossover in the diffusion. Currently, we are investigating the corresponding quantum system.