Nonlinear Excitations in Bose-Einstein Condensates

Introduction

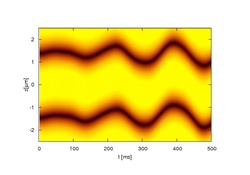
Ultracold atomic gases in the condensed phase represent macrosopic quantum states of many-body systems that can be described theoretically on a mean-field level by the so-called Gross-Pitaevskii equation. The latter extends the nonlinear Schroedinger equation thereby including mesoscopic environments such as traps. Our focus in these systems are nonlinear excitations. For quasi one dimensional systems the lowest excited states are solitonic states.

Solitons occur in various systems with nonlinear interaction such as in water waves, in fiber optics or in magnets. They have got amazing properties. Solitons are localized. While propagating they do not change their shapes. They can interact with each other and emerge from the collision unchanged except for a phase shift. We use ultracold atomic gases to model various setups in order to improve the understanding of the behavior of solitons. We develop simple models describing solitons, their mutual interaction and their interaction with the environment.

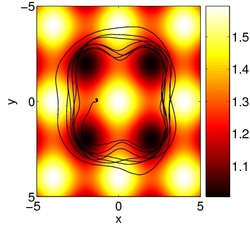
The two dimensional equivalent of a soliton is a vortex. The most famous vortex in nature is probably the tornado. However vortices occur in many different systems. We investigate vortices and their properties in cold atomic gases and develop models to describe the interaction of vortices in different surroundings. One of the most astonishing attributes of cold atoms is that one can tune the interaction between the atoms via so-called Feshbach resonances. It is even possible to prepare systems with spatially varying collisional interaction. We investigate effects of a spatially dependent interaction on the ground state of a Bose-Einstein Condensate and on excited states.

This work is done in close collaboration with other theoretical groups (D. Frantzeskakis, Athens, and P. Kevrekidis, Amherst).