Kaleidoscope
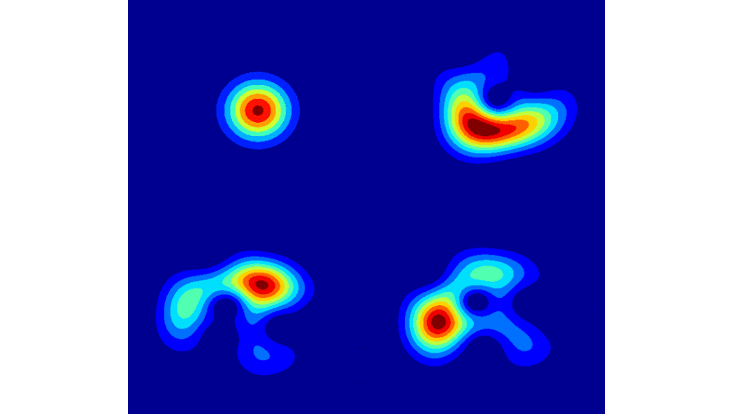
Photo: AG Schmelcher
The Husimi-Q distribution at different times allows for the investigation of phase space dynamics.

Photo: AG Schmelcher
Phase profile evolution of a higher order natural orbital corresponding to an ab initio quantum dynamics simulation of a bosonic many-body system out of equilibrium.
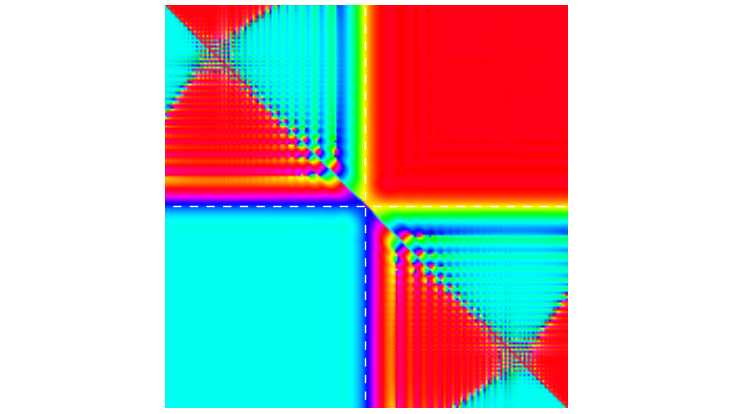
Photo: AG Schmelcher
Spatial phase distribution of a certain natural geminal, i.e. eigenvector of the reduced 2-body density operator, for a bosonic many-body system in a non-equilibrium state.
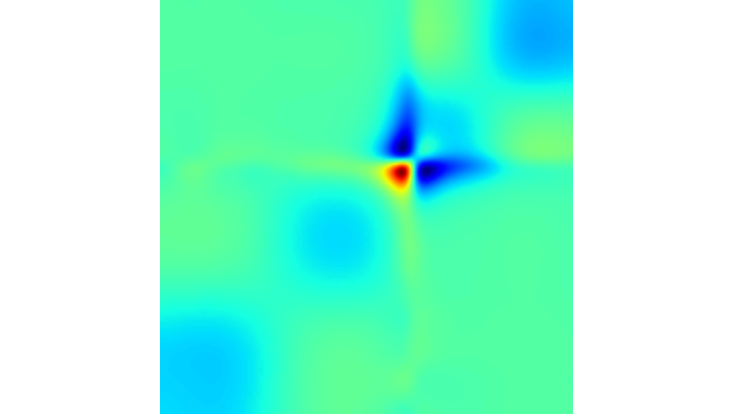
Photo: AG Schmelcher
Two-body correlation function of a decaying grey matter-wave soliton.
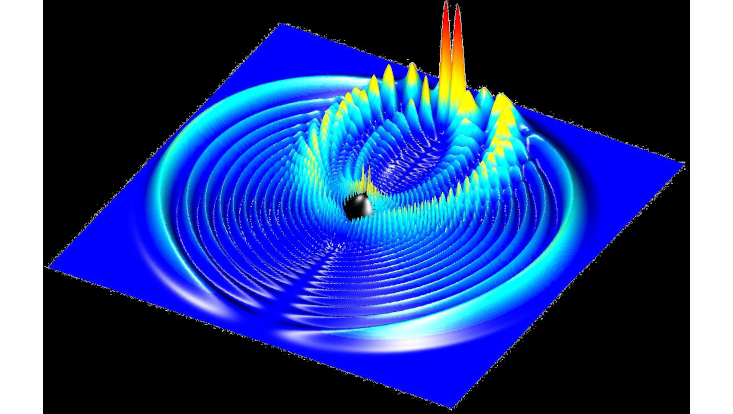
Photo: AG Schmelcher
Trilobite state: The electron probability density of a 35s Rydberg molecule.
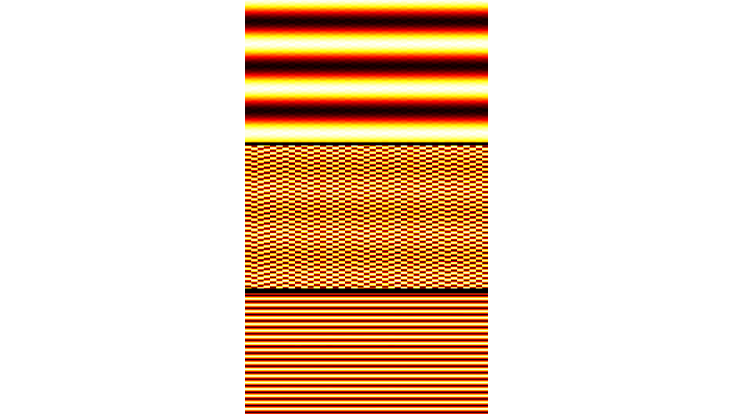
Photo: AG Schmelcher
The relaxation of a nonlinearly excited chain of particles in a lattice towards its equilibrium configuration gives rise to collective behavior in terms of oscillation patterns. The figure shows extracts from the time-evolution of the chain's velocity distribution.
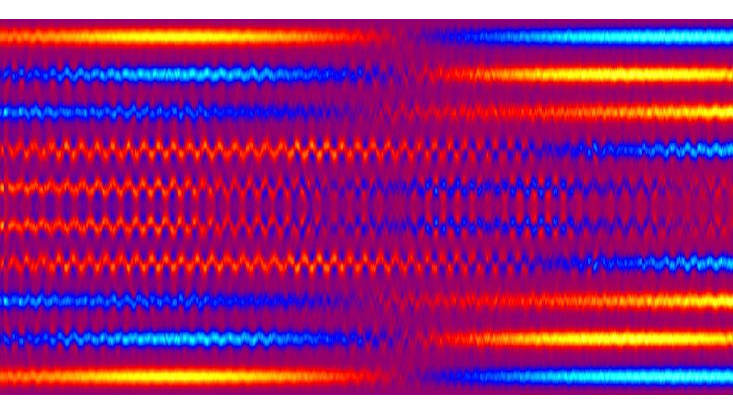
Photo: AG Schmelcher
The fluctuations of the one-body density evolution for five repulsive bosons in a lattice potential with ten wells, after a sudden change in the interaction strength (quench).
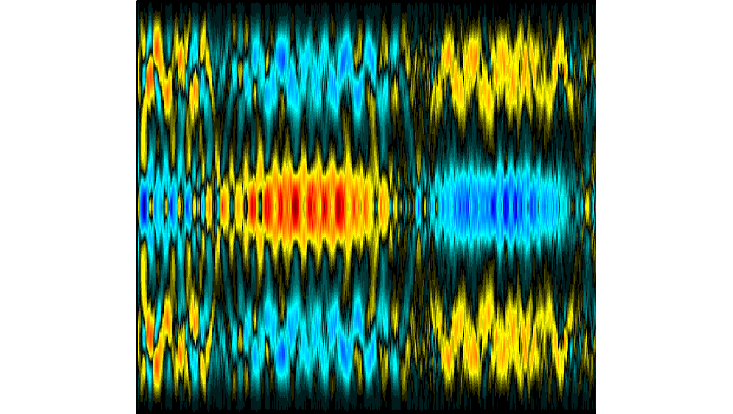
Photo: AG Schmelcher
The fluctuations of the one-body density evolution (small time-scales) for four repulsive bosons in a lattice potential with three wells, after an abrupt change in the interaction strength (quench).

Photo: AG Schmelcher
An electron wave flowing through an open, half-elliptical quantum billiard with four leads, in a strong magnetic field. Coming in through the leftmost lead, the electron forms an edge state which circulates around an obstacle in the middle.

Photo: AG Schmelcher
Directed current: Electron waves injected in each port of an open quantum billiard are transmitted selectively to other ports by tuning a perpendicular magnetic field from zero (top) via intermediate (middle) to high strength (bottom row).

Photo: AG Schmelcher
Energy spectrum of a soft-wall elliptic quantum billiard as a function of magnetic field strength (horizontal axis), plotted on top of the transmission function for the same system attached to left and right leads.
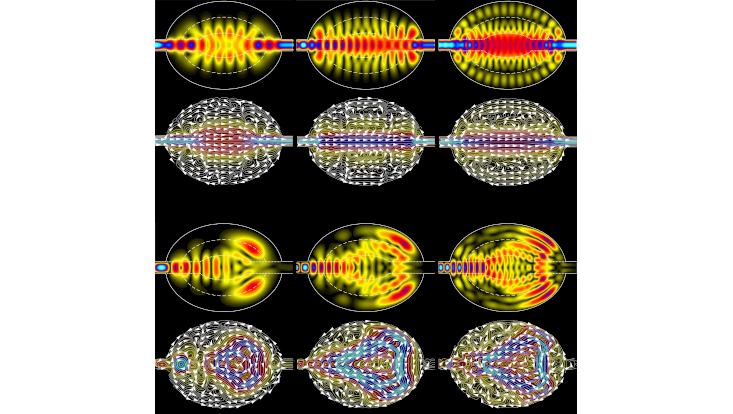
Photo: AG Schmelcher
Probability density and current density streamlines of electrons in an open soft-wall quantum billiard forwardly collimated in zero magnetic field (top) and backscattered at finite field strength (bottom), persistently in increasing energy (left to right).
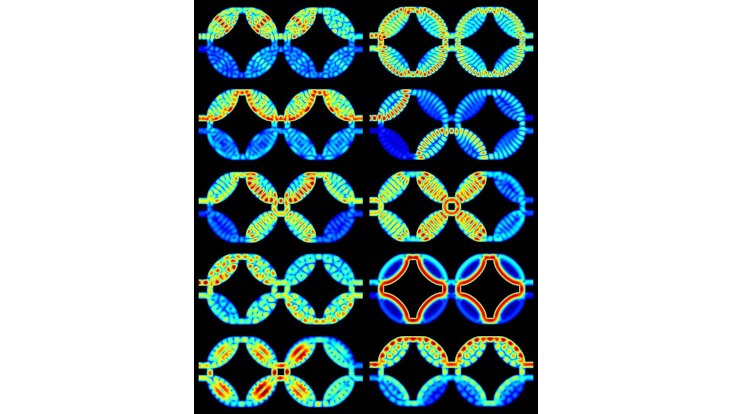
Photo: AG Schmelcher
Local density of states for electron waves flowing through a four-terminal lattice of elliptic quantum dots (ingoing wave in the upper left lead), at different energies and applied magnetic field strengths.
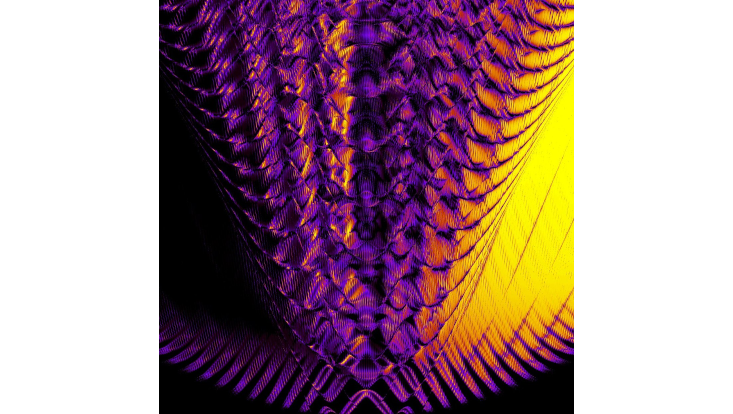
Photo: AG Schmelcher
Transmission as a function of energy (vertical axis) and magnetic field (horizontal axis) for electron waves flowing through a four-terminal lattice of elliptic quantum dots (see previous picture) from the upper left to the upper right lead.

Photo: AG Schmelcher
Extract of the phase space portrait of two superimposed simultaneously oscillating lattices, with different lattice spacings.

Photo: AG Schmelcher
A Quantum Billiard is a two-dimensional closed region where waves are confined. Here, the first hundred oscillation modes are shown for an oval quantum billiard with left and right stubs.
Photo: AG Schmelcher
A Quantum Billiard is a two-dimensional closed region where waves are confined. Here, the first hundred oscillation modes are shown for an oval quantum billiard with left and right stubs.
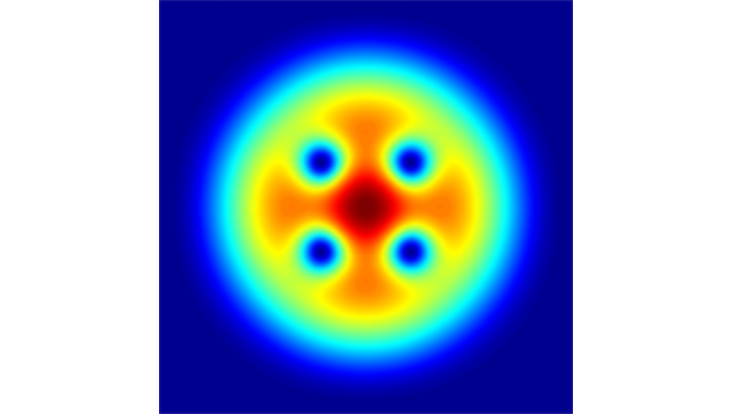
Photo: AG Schmelcher
In a Bose-Einstein condensate, millions of ultracold bosonic atoms cooperate to form a superfluid. Stirring this superfluid excites quantized vortices. The picture shows the simulated density profile of a condensate cloud with four such vortices.

Photo: AG Schmelcher
Extract of the phase space portrait of an oscillating lattice.
Photo: AG Schmelcher
Scattering function of oscillating potential barrier.
Photo: AG Schmelcher
Attraction to periodic orbits in the driven lattice.
Photo: AG Schmelcher
Floquet Mode in a phase modulated driven lattice.

Photo: AG Schmelcher
Local invariants in an imperfect lattice.

Photo: AG Schmelcher
Repulsive ions constrained to move on a toroidal helix can stabilize in many different configurations. Here eight such patterns are seen from above.
Photo: AG Schmelcher
Trajectories resulting from the scattering of two charged particles confined on an inhomogeneous helix for various values of initial energy, as viewed in the relevant two-particle space.
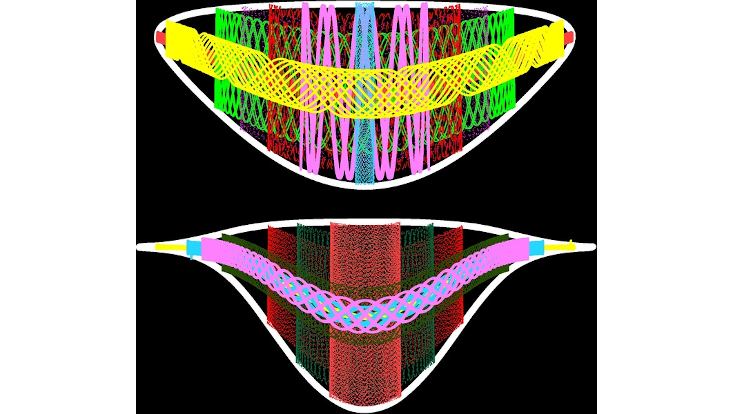
Photo: AG Schmelcher
Bounded trajectories resulting from the scattering of two charged particles confined on an inhomogeneous helix, as viewed in the relevant two-particle space, for a lower (upper) and a higher (lower) energy.
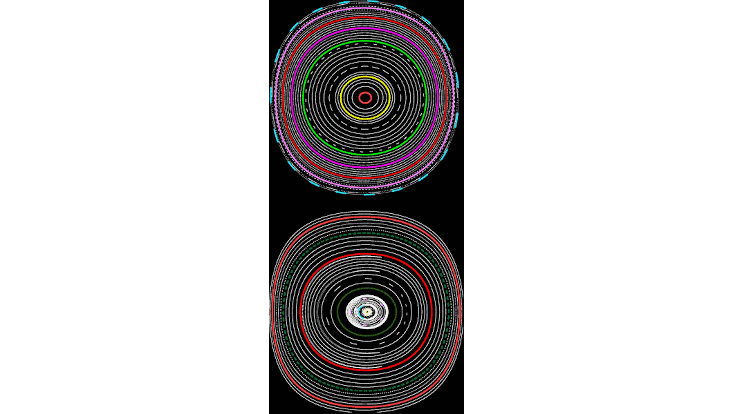
Photo: AG Schmelcher
Poincaré surfaces of section for bounded trajectories resulting from the scattering of two charged particles confined on an inhomogeneous helix, for a lower (upper) and a higher (lower) energy.
