Quantum Computing and Quantum Algorithms

Over the past few decades, the study and control of quantum systems have evolved significantly, paving the way for their application in modern technology. The rise of quantum computing, both in theory and experiment, has opened up new avenues for exploring quantum algorithms, piquing interest from the scientific community and the industry alike. However, one of the biggest challenges in the current era of quantum computing is the limited availability of resources, particularly the number of controllable qubits. This limitation makes the development of efficient quantum algorithms that can accurately solve optimization problems a crucial area of research.

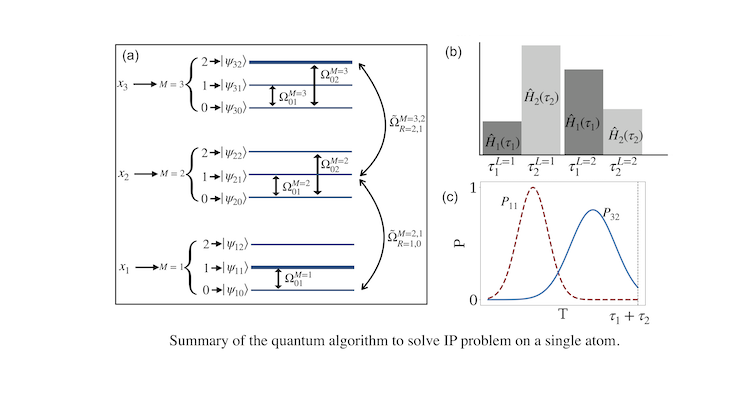
Efficiency refers to the ability to encode complex mathematical problems onto a quantum system with a limited number of qubits, and accuracy corresponds to the reliability of the output of the quantum algorithm. Our work aims to address both of these challenges by developing new quantum algorithms for relevant optimization problems. To this end, we focus on a broad class of NP-hard problems, which are often expressed as quadratic unconstrained binary optimization (QUBO) or integer programming (IP). Notable QUBO problems, such as maximum cut (Max-cut) and maximum independent set (MIS) are mapped onto a system of interacting Rydberg atoms, with solutions obtained through quantum annealing in conjunction with optimal control methods. In the spirit of developing efficient algorithms, we exploit the concept of quantum parallelism to solve an IP problem on a single atom, which is the first of its kind. We developed these algorithms with the goal of extending them to address more complex and larger-scale problems, further enhancing their applicability.