Successful suppression of servo bumps by more than 20 dB

12 September 2023

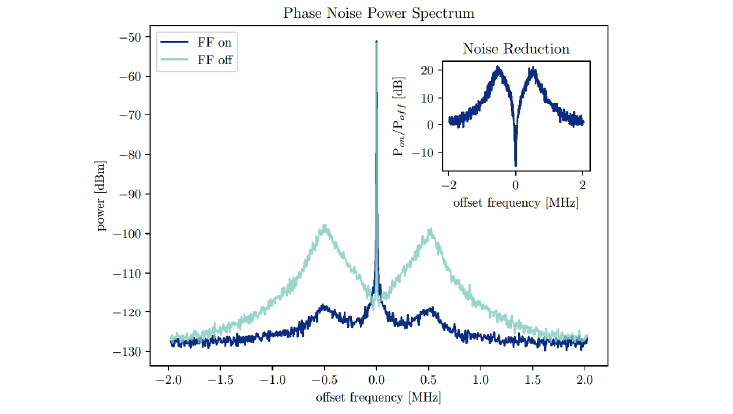
Photo: UHH / Herbig

Comparison of the noise spectrum of the Rydberg laser with and without servo bump suppression.

Philipp Herbig has successfully finished his Bachelor’s project on the topic of servo-bump phase noise suppression.

Quantum computing and simulation experiments based on neutral atoms require highly-stable laser frequencies for resonant excitation. This is typically achieved with a Pound-Drever-Hall (PDH) locking scheme, narrowing the laser linewidth and stabilising the frequency against long-term drifts. However, this feedback scheme necessarily creates servo bumps, which can severely limit excitation fidelities if the servo bandwidth is on the same order of magnitude as the Rabi frequency. A feed-forward scheme to suppress these servo bumps was first shown by Li et al. [1], and is here implemented in our Ytterbium-based quantum-computing experiment.

Our experiment is being set up to trap neutral ¹⁷¹Ytterbium atoms in optical tweezers. The two nuclear spin states in the ¹S₀ ground and ³P₀ metastable state can be used as natural qubits. We use light at a wavelength of  301.5 nm to excite the metastable atoms to an (n>50) ³S₁ Rydberg state to entangle two neighbouring qubits within a blockade radius, with expected Rabi frequencies on the order of MHz.

A 1206 nm laser, the quadruple fundamental of our Rydberg-excitation laser, was first frequency-stabilised to a cavity with finesse 5000 using a PDH lock to a linewidth of about 3 kHz. The servo bumps, about 500 kHz away from the carrier, however, are not present in the cavity transmission light of the cavity. Within this scheme [1], this light is compared to the unfiltered light using a heterodyne measurement. The resulting phase information is then used to feed-forward the inverse of these phase deviations to an EOM via an optical dealy line. This way, the phase noise originating from the PDH-lock was decreased by −20 dB. Finally, fibre-noise cancellation was implemented to compensate for acoustic phase noise picked up by optical fibres.

[1] Li et al., PRA 18, 064005 (2022)