Integer programming using a single atom

5 November 2024

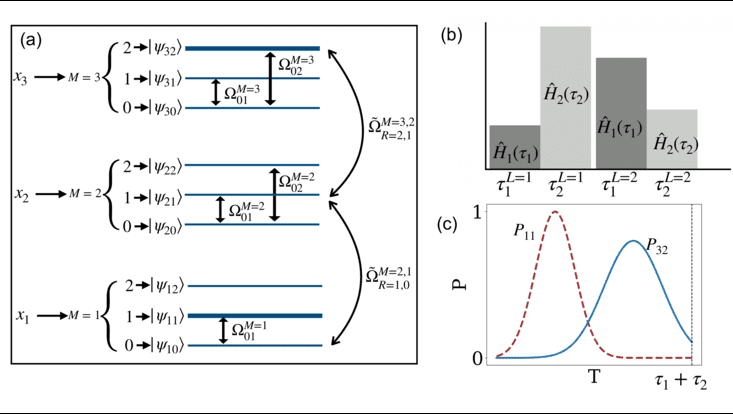
Photo: AG Schmelcher

Depiction of the quantum algorithm for solving the IP problem using a multi-level system.

Integer programming (IP) is a variable assignment problem commonly used for formulating industry- related optimization problems. Generally, any real-world problem such as warehouse assignment possesses discrete variables and multiple restrictions on these variables, and they are often mapped to an IP containing integer variables and constraints respectively. Solving such a problem is a classi- cally difficult task (NP-hard) yet important for optimization, thus serving as a prototype problem for quantum computation. However, current quantum algorithms for IP are inefficient as they involve mapping integer variables to qubits that behave as interacting spins. This poses a significant challenge of dealing with a much larger number of qubits as compared to the number of integer variables in the problem which are noisy as well. Solving IP directly on quantum systems without going through the route of encoding to qubits has not been attempted and is an open area of research.

In this work, we present a direct algorithmic implementation of both linear and non-linear IP problems, utilizing a single atom to handle a finite number of variables and constraints. The integer values of the variables are associated with having a non-zero population of different internal levels of an atom.  The  key idea of our framework is to access different energy manifolds of the atom with tunable external fields resulting in a selective superposition of states representing the IP problem altogether. By employing optimal control techniques, the strength and the time for these external fields are optimally tuned to fulfill the constraints as well as maximize the cost function of the problem. In our simulations, the solutions to varying prototypical IP problems are successfully found within a few microseconds. Any quantum system with multiple controllable degrees of freedom can serve as a platform for experimental realization. These include the simulation of synthetic dimensions and the multi-level system of a Rydberg atom, all of which are readily available with present-day technology.

Publication

Publication
K. Goswami, P. Schmelcher and R. Mukherjee

"Integer programming using a single atom"

Quantum Science and Technology 9, 045016 (2024)