Quantum Hidden Symmetries

27 April 2021

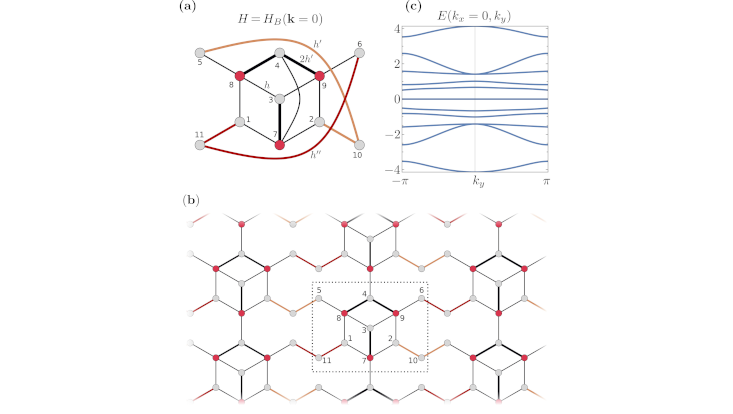
Photo: AG Schmelcher

(a) Graph representation of the Bloch Hamiltonian of the lattice in (b) with energy band structure shown in (c). The graph has no geometrical symmetry, but at zero quasimomentum (k = 0) it features a latent non-abelian symmetry involving the red sites (labeled 7,8,9), explaining the observed two-fold degeneracies in the band structure.

Symmetries are of fundamental importance for the understanding and modeling of physical systems, virtually across all length and energy scales. In particular, symmetries may induce degeneracies in the frequency spectrum of wavemechanical systems. Researchers at the Center for Optical Quantum Technologies of the University of Hamburg have demonstrated a novel route to address symmetry-induced degeneracies, by exploring certain hidden symmetries in discrete and lattice-like models. Such so-called "latent symmetries" are generally unveiled when reducing a system’s description to a suitable effective model without affecting its eigenspectrum. They may therefore be used to explain, e.g., energy degeneracy points which occur in band structures and whose symmetry origin is obscured at first sight.

The occurrence of degeneracy - more than one different eigenstates of a system’s Hamiltonian having the same eigenenergy - underlies a multitude of phenomena in atomic, molecular, and condensed matter physics. The connection of degeneracy to symmetries of a system is provided within the framework of group theory, by investigating the transformations under which the system’s Hamiltonian remains the same. Degeneracy occurs when the group of symmetry transformations is non-abelian, with the degree of degeneracy coinciding with the group’s dimension. When a degeneracy cannot be attributed in this manner to an apparent symmetry, with an important example being the invariance of the setup under geometrical transformations, then it is usually considered "accidental" - at least until some type of hidden symmetry is discovered which explains it.
The researchers at the University of Hamburg have identified an alternative approach to explaining degeneracy by symmetry for the vast class of systems described by discrete model Hamiltonians, such as coupled sites in a lattice. It still invokes group theory, though applied to an effective Hamiltonian obtained from the original one by a dimensional reduction. The system’s eigenspectrum is thereby typically left intact. Symmetries of the reduced systemare then generally "latent" in the original one, in the sense that they are not directly visible as the invariance under geometrical transformations. If the latent symmetry has a non-abelian group representation, it automatically leads to corresponding spectral degeneracy. Latent symmetries were recently introduced in the mathematical theory of graphs, and the new connection to degeneracy is a promising aspect of applying graphtheoretical tools to study physical systems. Further, in the present work latent symmetries are shown to correspond to locally restricted symmetries in the powers of the Hamiltonian, in turn expressed via ensembles of so-called "walks" along the graph representing the Hamiltonian. This indicates that treating physical setups as graphs may offer valuable insight into their observable properties.

Publication

M. Röntgen, M. Pyzh, C. V. Morfonios, N. E. Palaiodimopoulos, F. K. Diakonos, and P. Schmelcher

"Latent Symmetry Induced Degeneracies"

Physical Review Letters 126, 180601