Flat bands by latent symmetry

31 August 2021

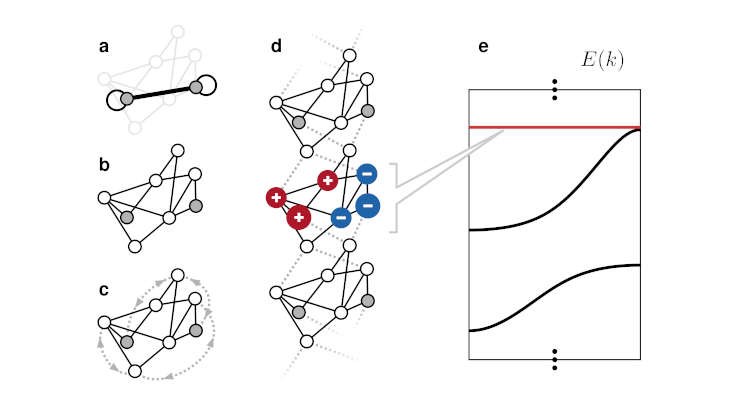
Photo: AG Schmelcher

(a) Isospectral reduction of the Hamiltonian visualized as a graph in (b) over two ``latently symmetric'' sites (gray), resulting in an exchange-symmetric effectife dimer Hamiltonian. (c) Bloch Hamiltonian of the lattice in (d), constructed by interconnecting (dotted lines) ``walk multiplets'' of the isolated unit cell. (e) Extract of the band structure of the lattice featuring a flat band corresponding to a compact localized state (amplitudes given by the size of the blue/red circles) with odd parity on the latently symmetric sites.

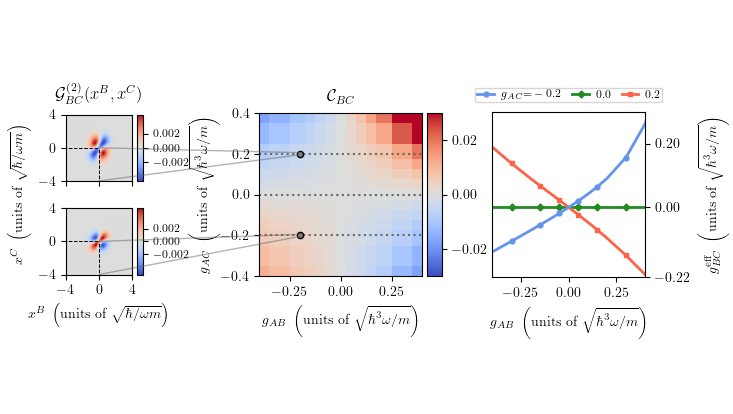
Flat bands of discrete lattice models are energy eigenvalue bands which are dispersionless, that is, independent of the crystal momentum. They play a pivoting role in designing systems with suppressed wave transport or dispersion and, more recently, in understanding strongly correlated states of matter and superconductivity. Flat bands originate from corresponding eigenstates which are compactly localized on only a small number of lattice sites and vanish on the rest of the lattice. Such compact localized states (CLSs) occur due to destructive interference of eigenstate amplitudes on surrounding sites, in turn caused by the special lattice geometry of the flat band system. A large effort has been made recently to identify schemes to generate CLSs and concomitant flat bands, a class of which relies on basic geometrical symmetries of the lattice unit cell. Using concepts and tools from spectral graph theory, researchers at the Center for Optical Quantum Technologies of the University of Hamburg have now demonstrated that a certain kind of hidden geometrical symmetries, called ``latent symmetries'', can be utilized to construct CLSs and flat bands. This opens up a new perspective on exploiting fundamental symmetry properties of model Hamiltonians to explain and design flat band systems.

Publication

C. V. Morfonios, M. Röntgen, M. Pyzh, and P. Schmelcher

"Flat bands by latent symmetry"

Phys. Rev. B 104, 035105 (2021) (Editor's Suggestion)