Parametrically excited star-shaped patterns at the interface of binary Bose-Einstein condensates

14 September 2020

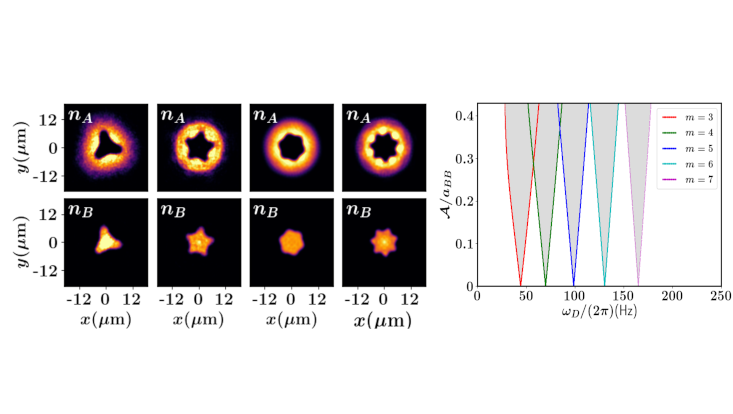
Photo: AG Schmelcher

Density profiles of the A (upper panels) and B (lower panels) component of the binary mixture illustrating the zoo of the m-fold star-shaped patterns at specific time-instants of the dynamics. The latter is induced by following a time-periodic modulation of the intercomponent scattering length. In the most right panel shown are the instability tongues, predicted within Floquet theory, for the first few sub-harmonic excitations of different azimuthal wavenumbers.

Liquid drops being weakly affixed to a vertically oscillating surface can display star-shaped patterns. This symmetry breaking mechanism of both the spatial and the temporal symmetries dates back to 1831 of the original Faraday experiment for a fluid in a vertically shaken vessel. In direct correspondence to this experiment, such symmetry-breaking related instabilities have been extensively investigated in diverse contexts including classical fluids, periodically modulated chemical systems, granular media, nonlinear fiber optics and within the realm of Bose-Einstein condensates (BECs).

A crucial observation here is that the dominant wavelength of the relevant instability, and the symmetries of the spontaneously generated patterns are specifically determined by a few intrinsic properties of the liquid such as its density and surface tension. Accordingly, multicomponent BECs exhibiting a well-defined interface offer a versatile platform  to emulate various interfacial tension triggered fluid instabilities with the underlying interfacial tension stemming from the combined effect of quantum pressure and intercomponent interactions. These instabilities, for instance, manifest as the Rayleigh-Taylor type, the capillary, the Kelvin-Helmholtz, the Richtmyer-Meshkov, the countersuperflow, and the Rosensweig instability as well as the Benard-Von-Karman vortex street.

In this work, we unravel such a Faraday-wave parametric instability leading to pattern formation at the interface of harmonically trapped radially phase-separated binary BECs. The  emergent star-shaped configurations, see Fig. 1, are generated either with the aid of a time-periodic modulation of the involved scattering lengths or utilizing a vibration of the two-dimensional trap. To be concrete, we showcase that the sub-harmonically oscillating interface possesses m-fold rotational symmetries which can be in turn controlled by the characteristics of the modulation protocol, namely its strength and frequency. To further explicate the emergence and origin of the resulting patterns, we derive an effective Mathieu equation allowing us to infer a dispersion relation for the natural angular frequencies and predict the generated interfacial tension of the mixture [right most panel of Fig. 1]. Remarkably, it is demonstrated that this dispersion relation can be employed to predict the interfacial tension of the phase-separated BEC. Our work paves the way for ongoing ultracold atom experiments to predict the interfacial tension and emulate phenomena of a liquid drop weakly pinned to an oscillating surface.

Publication

D.K. Maity, K. Mukherjee, S.I. Mistakidis, S. Das, P.G. Kevrekidis, S. Majumder, and P. Schmelcher,

“Parametrically excited star-shaped patterns at the interface of binary Bose-Einstein condensates”

Physical Review A 102, 033320 (2020)