Entanglement Induced Interactions in Binary Mixtures

26 July 2018

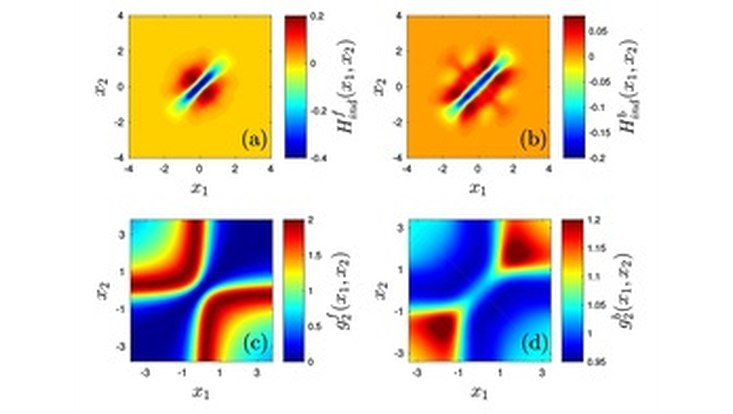
Photo: AG Schmelcher

FIG. 1. Upper panels: The induced interactions among the fermions (a) and the bosons (b). Lower panels: The pair-correlation functions for the fermionic (c) and the bosonic (d) species.

Induced interaction has become a major concept to understand and simplify the physics of systems with two types of particles, so-called binary mixtures. An important example is the formation of Cooper pairs in a crystalline solid.

Here, two electrons may acquire an attractive interaction by the exchange of phonons owing to the lattice vibrations. However, the discussion of such a concept is usually restricted to the many-particle limit and to homogeneous infinitely extended systems. Moreover, the role of interspecies entanglement and its relation to the induced interactions represents an open question.

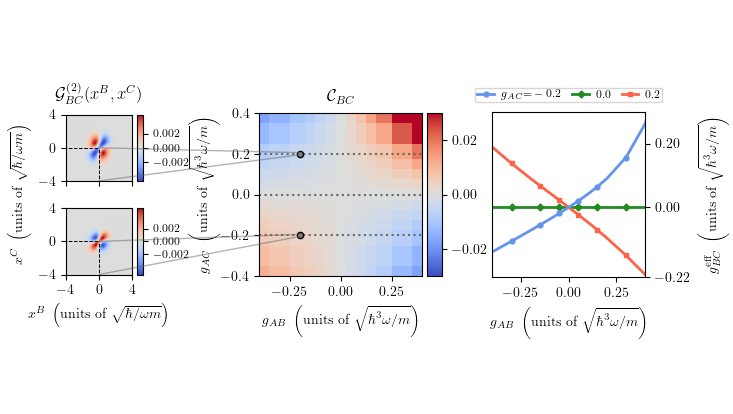
In our recent work, we fill this gap by establishing a general conceptual framework for the identification and the characterization of induced interactions in binary mixtures. In particular, we reveal how interspecies entanglement creates the induced interactions. Furthermore, we derive a general expression for the effective single-species Hamiltonians of both subsystems which not only introduces a significant simplification but also opens-up the possibility for in-depth studies of mixtures. Moreover, our approach naturally incorporates few-body and inhomogeneous systems extending the concept of induced interactions beyond its current scope. Employing the example system of a few-body ultracold Bose-Fermi mixture, we obtain induced Fermi-Fermi and Bose-Bose interactions [cf. Figs. 1(a) and 1(b)] with short-range attraction and long-range repulsion. With this, we show how beyond mean-field physics visible in the pair-correlation functions [cf. Figs. 1(c) and 1(d)] can be understood via the induced interactions.

Physical Review Letters 121, 043401 (2018)