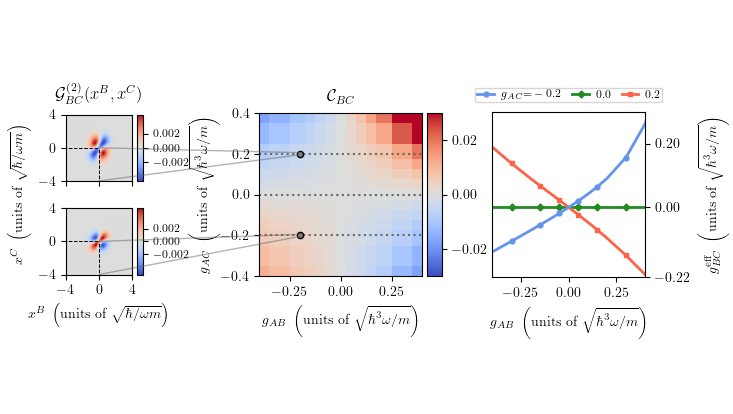
Quantum Physics
Control of flat bands using local symmetries
30 January 2018
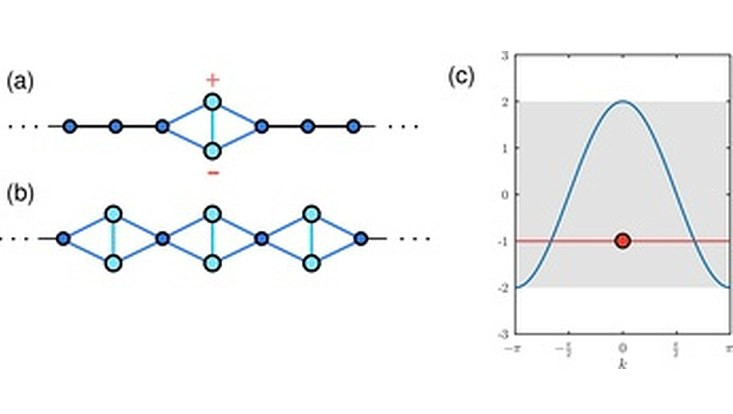
Photo: AG Schmelcher
The electronic band structure is one of the most important tools in the studies of crystals. Using band theory, phenomena such as optical absorption and electrical conductivity can be explained.
The core element of modern electronic devices, the transistor, is also based on the study of band structures. Usually, the band structure of a crystal is a rather complicated landscape, and the bands are of curvy shape. However, in some cases a crystal may feature a completely flat band. Due to its flatness, the effective mass of an electron in this band is infinite. Apart from this remarkable effect, flat bands are of great interest in the study of many-particle systems, where they can be used to facilitate interactions between these particles. Moreover, the famous fractional Quantum Hall effect is based on the existence of flat bands. On a technological side, optical flat bands might be used to facilitate efficient information transfer in arrays of coupled waveguides, as they could be used in future all-optical computers.
In our recent work, we draw a connection between certain classes of locally symmetric structures to the emergence of flat bands. To this end, we analyze so-called tight-binding systems. Here, the system is modelled by discrete points (the atoms) interacting with each other through short-ranged couplings, usually called 'hoppings'. In such systems, the emergence of a so-called compact localized state is possible, which has strictly zero amplitudes outside a small region. If each unit cell of a crystal can host such a state, a flat band emerges. Interestingly, it is possible to perturb an otherwise perfect crystal such that a compact localized state is created. If designed carefully, such a state does not interact with the states in the dispersive bands. Then the states is a so-called bound state in the continuum, an exciting case which could, for example, be used to store information within a crystal.