Research
The physical properties of a solid are largely determined by the dynamics of its electrons. These electrons represent the driving force for phenomena such as magnetism, (super)conductivity or polarizability, which are potentially also relevant for practical applications. Of particular technological interest are materials with strong correlation effects originating from the Coulomb repulsion between the particles. However, the theoretical description of such correlated electron systems is challenging due to the large number of interacting particles (Avogadro number NA~1026). In our research group we address this problem by developing quantum field theoretical methods to solve the complicated many-body problem.
Green's functions
Green's functions describe the response of a correlated many-body system to external perturbations such as electric and magnetic fields, pressure or changes in temperature. Of particular high interest are the one- and two-particle Green's functions as the allow for the calculation of physical observables which are also experimentally accessible. Typically, one is interested in the parts of the Green's functions which describe the interaction (scattering, wiggled green lines in the following figure) between the particles. For a one-particle excitation ("1P level") this corresponds to the self-energy Σ while a two-particle excitation is described by a so-called vertex Γ: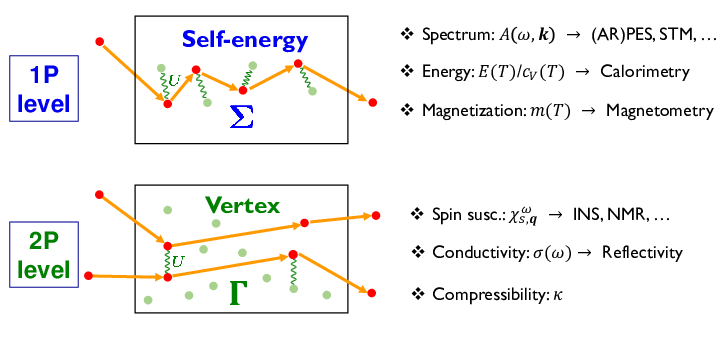 The physical observables, which can be obtained from the respective correlation function, are indicated on the right-hand side of this picture. In particular, the self-energy Σ gives access to the spectral function, the specific heat or the magnetization while the vertex Γ provides information regarding the spin susceptibility or the electrical conductivity. This vertex itself is a complicated object, which depends on the energies n and n' of the two electrons involved in a scattering event:
The physical observables, which can be obtained from the respective correlation function, are indicated on the right-hand side of this picture. In particular, the self-energy Σ gives access to the spectral function, the specific heat or the magnetization while the vertex Γ provides information regarding the spin susceptibility or the electrical conductivity. This vertex itself is a complicated object, which depends on the energies n and n' of the two electrons involved in a scattering event:
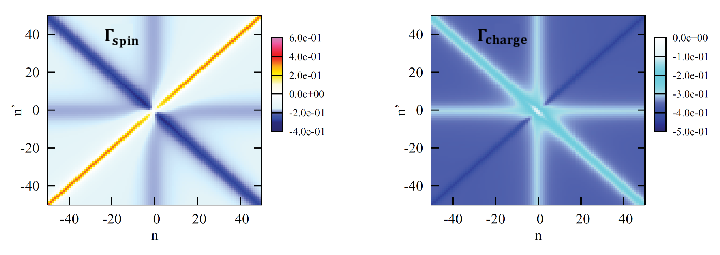 The different line structures in the spin and charge vertex correspond to spin, charge and particle-particle (pairing) fluctuations of the many body system.
The different line structures in the spin and charge vertex correspond to spin, charge and particle-particle (pairing) fluctuations of the many body system.
Calculation of the Green's functions - Feynman diagrams
The calculation of the Green's functions for a correlated many-body system represents one of the big challenges in theoretical solid-state physics. For small systems, this can be achieved by exact diagonalization of the many-body Hamiltonian or Monte-Carlo simulations. For realistic materials, for which these approaches are not applicable due to the large number of interacting particles, quantum field theoretical methods represent a powerful tool for the calculation of the Green's functions. Within this framework, the one- and two-particle correlation functions are obtained perturbatively from the non-interacting Green's functions and the interaction between the particles. The corresponding perturbation series can be represented graphically in terms of Feynman diagrams:
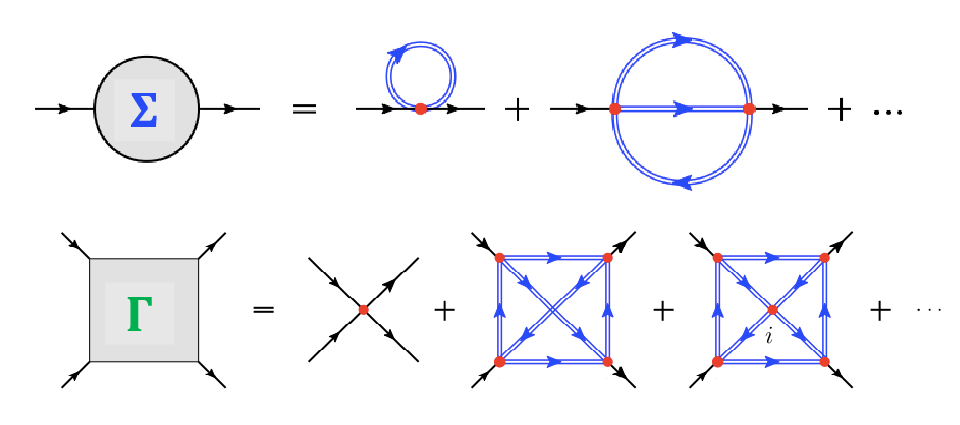 The blue double lines represent non-interacting Green's functions while the red dots correspond to the Coulomb interaction. Importantly, a specific physical meaning can be assigned to each of such diagrams. The choice of diagrams for the calculation of Σ and Γ is then dictated by the physical situation under consideration. In this respect, the dynamical mean field theory (DMFT) represents one of the most successful approaches in the last three decades. It describes all purely local correlation effects by considering all local Feynman diagrams for Σ, i.e., all diagrams where the interaction between the particles (red dots) takes place at the same point in space or at the same lattice site. Within our research activities, we develop diagrammatic extensions of DMFT, which include also non-local contributions, which is essential for the correct description of magnetism and superconductivity. An overview over these diagrammatic extensions of DMFT can found in a recently published article in Review of Modern Physics (Rev. Mod. Phys. 90, 025003, 2018).
The blue double lines represent non-interacting Green's functions while the red dots correspond to the Coulomb interaction. Importantly, a specific physical meaning can be assigned to each of such diagrams. The choice of diagrams for the calculation of Σ and Γ is then dictated by the physical situation under consideration. In this respect, the dynamical mean field theory (DMFT) represents one of the most successful approaches in the last three decades. It describes all purely local correlation effects by considering all local Feynman diagrams for Σ, i.e., all diagrams where the interaction between the particles (red dots) takes place at the same point in space or at the same lattice site. Within our research activities, we develop diagrammatic extensions of DMFT, which include also non-local contributions, which is essential for the correct description of magnetism and superconductivity. An overview over these diagrammatic extensions of DMFT can found in a recently published article in Review of Modern Physics (Rev. Mod. Phys. 90, 025003, 2018).
Physics of correlated electron systems - magnetism and superconductivity
Apart from the development of new methods, our research activities are devoted to the description and the understanding of physical phenomena which arise in strongly correlated electron systems. By means of the above-described techniques, we can numerically calculate and analyze interesting properties of such many-body systems. An overview over the wide range of applications is provided in the above-mentioned review article. An example for the capabilities of the developed methods is their applicability for the description of the physics of the cuprates. These compounds feature a layered crystal structure where planes containing copper and oxygen atoms, which are arranged in a quadratic lattice, alternate with layers containing heavy ions. The crystal structure of one member of this class of materials, i.e., La2CuO4, is depicted on the right-hand side of the following figure:
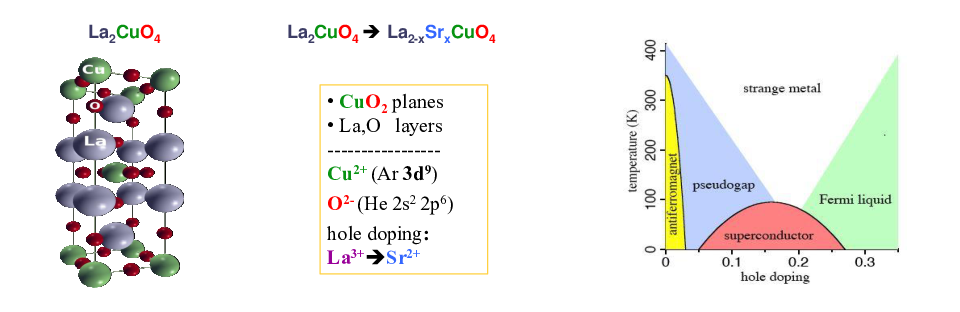 Replacing some of the La atoms with Sr atoms reduces the number of electrons in the Cu-O planes (hole-doping, see middle column of the figure). On the right hand-side of the figure, a generic temperature vs. doping phase diagram of this material is shown. One can identify an antiferromagnetic phase at low doping and a dome-shaped superconducting region at intermediate doping values as well as a paramagnetic phase at higher temperatures which features an unusual behavior due to correlation effects. Note that the superconducting state in this material extends to relatively high temperatures compared to more standard BCS superconductors. Therefore, this class of materials is attributed to the so called high-temperature superconductors which are also of high technological relevance.
Replacing some of the La atoms with Sr atoms reduces the number of electrons in the Cu-O planes (hole-doping, see middle column of the figure). On the right hand-side of the figure, a generic temperature vs. doping phase diagram of this material is shown. One can identify an antiferromagnetic phase at low doping and a dome-shaped superconducting region at intermediate doping values as well as a paramagnetic phase at higher temperatures which features an unusual behavior due to correlation effects. Note that the superconducting state in this material extends to relatively high temperatures compared to more standard BCS superconductors. Therefore, this class of materials is attributed to the so called high-temperature superconductors which are also of high technological relevance.
By means of the above discussed diagrammatic methods it has been possible to calculate the phase diagram theoretically (see PRB 101, 075109, 2020) achieving a good agreement with experimental findings:
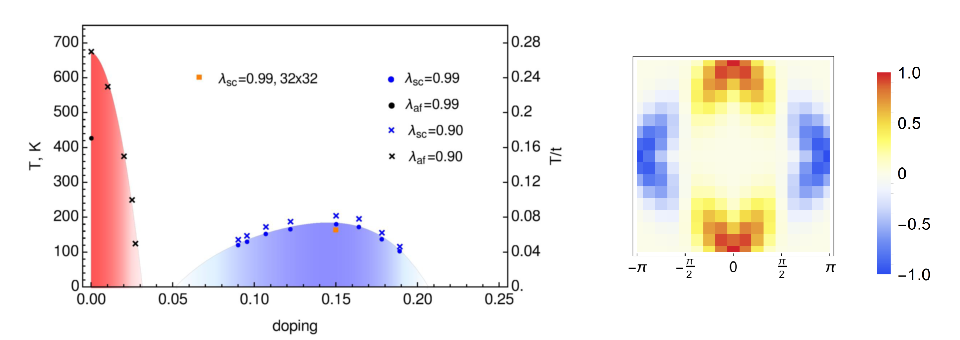 Moreover, the theoretical results provide crucial insights into the physical mechanisms which lead to this phase diagram. In particular, we have shown the spin fluctuations (and not, as usual, phonons) provide the pairing glue, i.e., an effective attractive interaction, between the electrons, which facilitates superconductivity. As a consequence, we observe a d-wave (instead of a s-wave) structure of the particle pairs which is illustrated on the right-hand side of the figure. These results demonstrate that quantum field theoretical methods indeed allow for the description of complex materials.
Moreover, the theoretical results provide crucial insights into the physical mechanisms which lead to this phase diagram. In particular, we have shown the spin fluctuations (and not, as usual, phonons) provide the pairing glue, i.e., an effective attractive interaction, between the electrons, which facilitates superconductivity. As a consequence, we observe a d-wave (instead of a s-wave) structure of the particle pairs which is illustrated on the right-hand side of the figure. These results demonstrate that quantum field theoretical methods indeed allow for the description of complex materials.
Future perspectives and research plans
The ongoing research activities in our research group consist in an improvement of the theoretical and numerical tools as well as the extension of these methods to a broader field of physical problems. This includes, among others:
- Development of improved methods which avoid inconsistencies in the calculation of physical observables
- Extension of the methods to multi-band systems
- Extension of the methods for non-equilibrium states of matter (dynamics)
- Investigation of correlation effects in topological states of matter
These research plans are carried out in the framework of the Emmy Noether project "Two-particle self-consistency in diagrammatic theories for strongly correlated electron systems".
