Forschung

Das Verhalten von Elektronen in einem Festkörper bestimmt maßgeblich dessen physikalische Eigenschaften. Insbesondere sind die Elektronen verantwortlich für Phänomene wie Magnetismus, (Supra)Leitfähigkeit oder Polarisierbarkeit, die auch für praktische Anwendungen sehr relevant sind. Von besonderem technologischem Interesse sind Materialien, in denen starke Korrelationseffekte aufgrund der Coulomb Abstoßung zwischen den Elektronen auftreten. Die theoretische Beschreibung solcher korrelierter Elektronensysteme ist wegen der großen Anzahl der wechselwirkenden Teilchen (Avogadro Zahl N_{A ~}10²⁶) sehr schwierig. In unserer Arbeitsgruppe entwickeln wir quantenfeldtheoretische Methoden zur Lösung dieses komplizierten Vielteilchenproblems.

Greensche Funktionen

Greensche Funktionen beschreiben die Antwort eines korrelierten Vielteilchensystems auf äußere Störungen wie zum Beispiel elektrische und magnetische Felder, Druck oder Temperaturänderungen. Von besonderem Interesse sind hierbei die Ein- und Zwei-Teilchen Greenschen Funktionen da sie die Berechnung physikalischer Observablen erlauben, die auch experimentell messbar sind. Üblicherweise ist man besonders an dem Anteil der Greenschen Funktion interessiert, der die Wechselwirkung (Streuung, grüne Linien in der folgenden Grafik) zwischen den einzelnen Teilchen beschreibt. Im Falle einer Ein-Teilchenanregung ("1P level") entspricht das der Selbstenergie Σ während die Zwei-Teilchenanregung ("2P level") durch den sogenannten Vertex Γ repräsentiert wird:

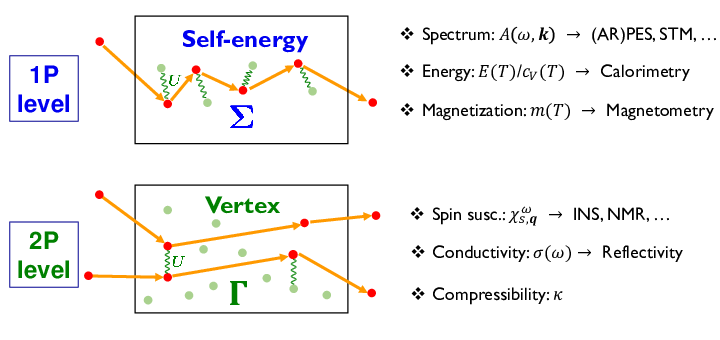Auf der rechten Seite des Bildes sind jeweils einige der physikalischen Observablen aufgelistet, die mittels der jeweiligen Korrelationsfunktionen bestimmt werden können. So erlaubt die Kenntnis der Selbstenergie Σ die Ermittlung der spektralen Funktion, der spezifischen Wärme oder der Magnetisierung während man vom Vertex Γ Informationen zur Spinsuszeptibilität oder elektrischen Leitfähigkeit erhält. Der Vertex selbst ist ein kompliziertes Objekt, das von den Energien n und n' der beiden aneinander gestreuten Elektronen abhängt:

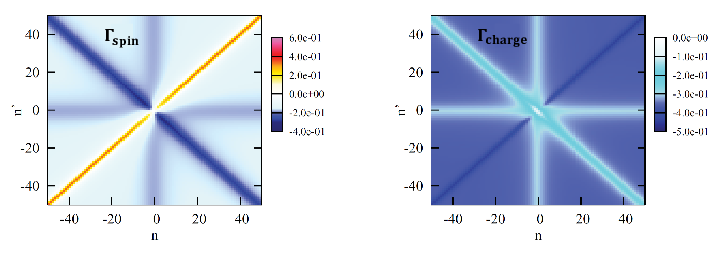
Die verschiedenen Linienstrukturen, die hier im Spin- bzw. Ladungs-Vertex beobachtet werden, entsprechen Spin-, Ladungs- und Teilchen-Teilchen-Fluktuationen des Vielteilchensystems.

Berechnung der Greenschen Funktionen - Feynman Diagramme

Die Berechnung der Greenschen Funktionen für ein korreliertes Vielteilchensystem stellt eine der großen Herausforderungen in der theoretischen Festkörperphysik dar. Für kleine Systeme kann dies durch numerische Rechnungen am Computer mittels exakter Diagonalisierung des Vielteilchen Hamiltonoperators oder durch Monte-Carlo Simulationen erreicht werden. Für realistische Materialien, bei denen die Anwendung solcher Verfahren wegen der großen Anzahl wechselwirkender Teilchen nicht möglich ist, stellen moderne quantenfeldtheoretische Methoden ein essenzielles Werkzeug für die Berechnung der Greenschen Funktionen dar. im Rahmen dieser Theorie werden die Ein- und Zwei-Teilchen Korrelationsfunktionen störungstheoretisch mittels der entsprechenden nicht-wechselwirkenden Greenschen Funktionen sowie der Wechselwirkung zwischen den Teilchen ermittelt. Die dabei entstehende Störungsreihe kann sehr anschaulich in Form von Feynman Diagrammen dargestellt werden:

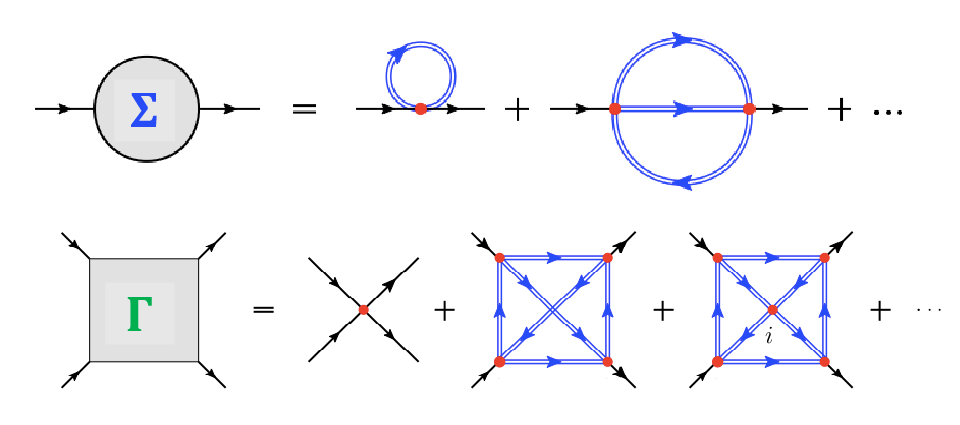
Die blauen Doppellinien stellen hierbei nicht-wechselwirkende Greensche Funktionen dar während die roten Punkte die Coulombwechselwirkung repräsentieren. Jedem solchen Diagramm kann eine spezifische physikalische Bedeutung zugeordnet werden. Die Auswahl der Diagramme, die man für die Berechnung von Σ und Γ berücksichtigt, ergibt sich dabei aus der physikalischen Situation, die man beschreiben möchte. In dieser Hinsicht stellt die dynamische Molekularfeldtheorie (DMFT) einen der erfolgreichsten Ansätze der letzten drei Jahrzehnte dar. Sie beschreibt alle lokalen Korrelationseffekte exakt indem sie alle lokalen Feynman Diagramme für Σ berücksichtigt, d.h., alle Diagramme bei denen die Wechselwirkung zwischen Teilchen (roter) Punkt am selben Ort (Gitterplatz) stattfindet. Im Rahmen unserer Forschungstätigkeit entwickeln wir diagrammatische Erweiterungen der DMFT, welche auch die Beiträge nicht-lokaler Korrelationseffekte miteinbeziehen, was vor allem für die korrekte Beschreibung von Magnetismus oder Supraleitung eine essenzielle Rolle spielt. Eine Übersicht über diese diagrammatischen Erweiterungen der DMFT ist in einem kürzlich veröffentlichen Artikel im Journal Review of Modern Physics zu finden (Rev. Mod. Phys. 90, 025003, 2018).

Physik korrelierter Elektronensysteme - Magnetismus und Supraleitung

Neben der Methodenentwicklung stellt die Untersuchung physikalischer Phänomene, die in stark korrelierten Elektronensystemen auftreten, den Hauptbestandteil der Forschungsaktivitäten der Arbeitsgruppe dar. Mit den oben beschriebenen Verfahren können interessante Eigenschaften solcher Vielteilchensysteme numerisch berechnet und analysiert werden. Eine Übersicht über die Vielzahl der Anwendungen findet sich im schon vorher erwähnten Reviewartikel. Ein Beispiel für die Leistungsfähigkeit der entwickelten Methoden ist deren Anwendbarkeit für die Beschreibung der komplizierten Physik der Kuprate.  Die Kristallstruktur dieser Klasse von Festkörpern ist schichtförmig aufgebaut, wobei sich eine Schicht  bestehend aus Kupfer und Sauerstoffatomen, die in einem quadratförmigen Gitter angeordnet sind, mit einer oder mehrerer Schichten von schwereren Elementen abwechselt (hier ist auf der linken Seite z.B. La₂CuO₄-auch LSCO genannt- schematisch dargestellt):

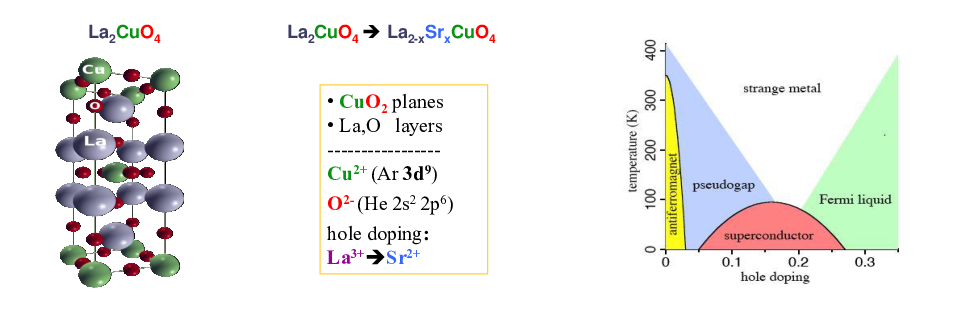
Ersetzt man in diesem Material La mit Sr, so findet man eine kleinere Anzahl von Elektronen in den Cu-O Ebenen (hole-doping). Ganz rechts ist ein generisches Phasendiagram dieses Materials als Funktion des Dopings und der Temperatur abgebildet, so wie es im Experiment gefunden wird.  Man kann eine (antiferro)magnetische und eine supraleitende Phase identifizieren sowie eine paramagnetische Phase bei höheren Temperaturen, die aufgrund von Korrelationseffekten sehr ungewöhnliche Eigenschaften aufweist. Da sich die supraleitende Phase bis zu sehr hohen Temperaturen erstreckt gehört dieses Material zur Gruppe der sogenannten Hochtemperatursupraleiter, welche auch von großer technologischer Relevanz sind.

Mittels der oben diskutierten diagrammatischen Verfahren ist es möglich dieses Phasendiagram theoretisch zu berechnen (siehe PRB 101, 075109, 2020), wobei eine sehr gute Übereinstimmung dem den experimentellen Ergebnissen erzielt werden konnte:

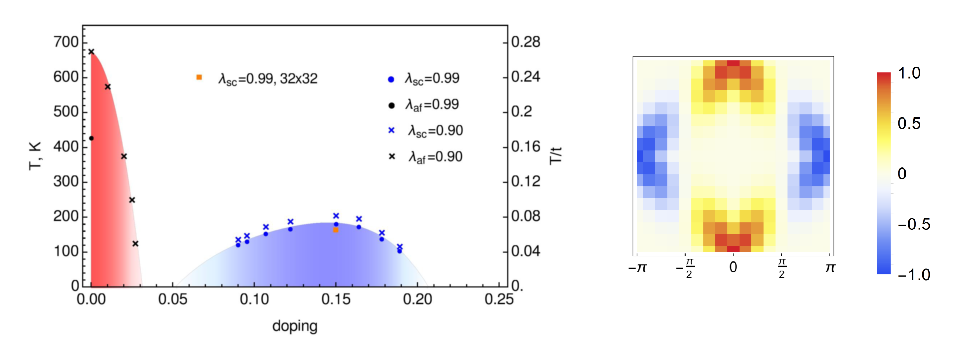
Des Weiteren erlauben die theoretischen Ergebnisse auch einen tieferen Einblick in die physikalischen Mechanismen, die zu diesem Phasendiagram führen. Insbesondere stellen Spinfluktuationen (und nicht die wie üblich Phononen) den "Kleber", also eine effektive anziehende Wechselwirkung zwischen den Elektronen, dar, der die Supraleitung ermöglicht. Das führt auch dazu, dass man es mit d-Wellen Supraleitung (statt wie üblich mit s-Wellen Supraleitung) zu tun was durch die geometrische Struktur der Wechselwirkung im rechten Teil des Bildes gezeigt wird. Diese Ergebnisse demonstrieren, dass es mit Hilfe quantenfeldtheoretischer Methoden in der Tat möglich ist die Eigenschaften komplexer Materialien zu beschreiben.

Zukünftige Forschungspläne und Perspektiven

Die laufende Forschungstätigkeit unserer Arbeitsgruppe besteht in der Verbesserung der verwendeten theoretischen und numerischen Methoden sowie der Erweiterung dieser Ansätze auf ein breiteres Feld physikalischer Probleme. Das beinhaltet unter anderem:

• Vermeidung von Inkosistenzen bei der Berechnung physikalischer Observable
• Erweiterung der Methoden auf Mehr-Band Systeme
• Erweiterung der Methoden zur Berechnung von Nichtgleichgewichtszuständen (Dynamik)
• Untersuchung von Korrelationseffekten in topologischen Zuständen der Materie

Diese Forschungsvorhaben werden im Rahmen des Emmy Noether Projekt „Zwei-Teilchen Selbstkonsistenz in diagrammatischen Theorien für stark korrelierte Elektronensysteme“ vorangetrieben.