Spin dynamic simulation

Life means change and change in magnetism means dynamics. However, spin dynamics is a great challenge in physics caused by the underlying nonlinear differential equations. These equations cannot be solved analytical in general.

Depending on the system size a quantum mechanical description is necessary or a classical one can be used. The goal of our group is to investigate the interface between classical physics and quantum mechanics. The used methods are identical: numerical solving of the equations of motion. The difference is just the choice of the differential equations: in the classical limit the Landau-Lifshitz-Gilbert (LLG) equation:

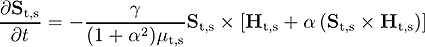
and in the quantum mechanical limit the time dependent Schrödinger equation (TDSE) with additional relaxation term [1]:

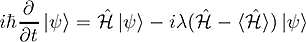
Both differential equations are describing the dynamics of a magnetic moment. The original LLG equation contains two parts : The first one describes the precession of the magnetic moment in an effective field 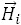(first term on the right hand side) and the second one the relaxation (second term). The last two terms have been proposed 60 years after the first mention and became of special interest during the last years.

These terms describe the coupling of the magnetic moment with a spin polarized current.

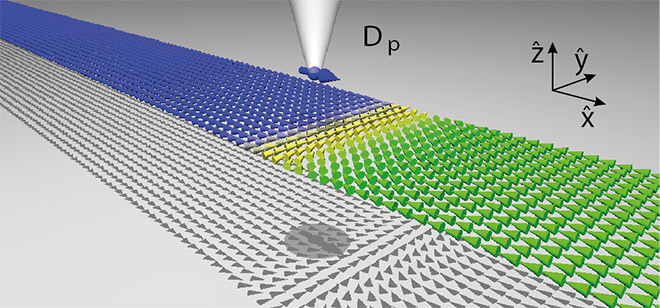
With this differential equation we could answer the question about the possibility of manipulation of a magnetic domain wall via a spin-polarized scanning tunneling microscope (SP-STM) [2-4]. Therefore, we have simulated a spin-polarized current tunneling from a magnetized tip to the sample a flat magnetic wire which contains a transverse domain wall. During the simulation the tip runs along the wire. It could be shown that it is possible to manipulate a domain wall with an SP-STM. To confirm this result additional Monte Carlo calculations have been performed showing identical results [3].

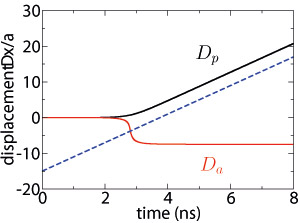
The dynamics cannot be described by the classical LLG equation if one goes to small systems e.g. magnetic molecules or single atoms. However, there are two exceptional cases: the dynamics of coherent states which behave classical and single spins described by a linear Hamilton operator [5]. Nevertheless, these are special cases. In general, one has to solve the TDSE or the quantum Liouville equation. We have used the TDSE to check the possibility to switch a single magnetic moment via a magnetic exchange force microscope (MEx-FM). Depending on the appearance of relaxation and quantum tunneling different scenarios can be described. Further, it can be shown that it is possible to switch the magnetic moment.