Algebraic Formulation Quantum Dynamics
The investigation of single magnetic atoms and magnetic clusters with a spin-polarized scanning tunneling microscope (SP-STM) raises the necessity of a quantum mechanical description of spin systems. The components of a spin, whose expectation values can be measured with an SP-STM, can be represented as elements of a local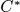 
-algebra 
.
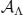The algebraic approach to Quantum Statistical Mechanics provides mathematically highly developed tools for a deep and fine analysis of physical systems. Within this framework quantum spin systems are modeled via a 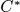-algebra 
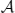with a net 
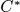of -subalgebras.
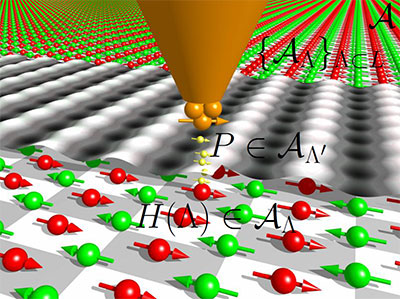
FIG. 1: The tip of the SP-STM induces a perturbation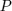 
of a nite system or a bouned derivation 
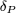for the innite case.
We are intereseted in applications of those mathematical tools to real systems, which are experimentally investigated with a SP-STM. Therefore we distinguish between a free unperturbed system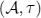 
with Hamiltonian H (e.g. magnetic atoms) and a perturbed system 
with Hamiltonian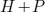 
(e.g. magnetic atoms plus SP-STM tip) depending on the situation if there is a perturbation 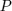induced trough the interaction between the tip and the sample or not. The finite temperature is considered in the free unperturbed or perturbed Kubo-Martin-Schwinger (KMS)-state 
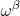or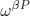 
characterizing the unperturbed or perturbed thermal equilibrium. The dynamics is given by the Heisenberg relations and described through a free unperturbed or perturbed one-parametric group of *-automorphisms 
or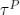 
acting on 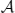. Depending on the physical situation the functions
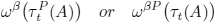
are applied. For the numerical calculations a self-developed computer program is used.
The abstract mathematical foundations can be found in the books Operator Algebras and Quantum Statistical Mechanics I+II.