Relaxation of a classical spin coupled to a strongly correlated electron system

13 September 2016

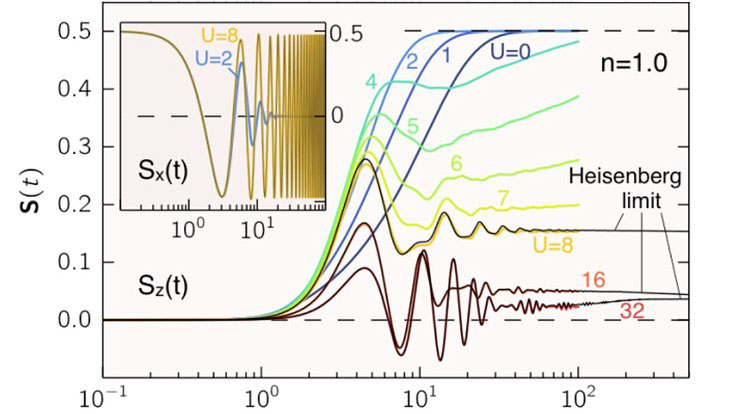
Photo: UHH/SFB925

A classical spin in an external magnetic field and antiferromagnetically coupled to a system of conduction electrons usually relaxes in the course of time and aligns to the field direction. We show that, if the conduction-electron system is strongly interacting, the real-time spin dynamics is highly unconventional since the two main electronic dissipation channels, namely transport of excitations via correlated hopping and via excitations of correlation-induced magnetic moments, become active on largely different time scales. It is demonstrated that correlations can even lead to a strongly delayed spin relaxation, which so far has been observed in purely electronic systems only.

A classical spin in a magnetic field B shows a precessional motion around the field direction with the Larmor frequency. If locally exchange-coupled to a large system of conduction electrons, the spin will precess but finally relax and align to the field direction. Approaching the local ground state, the energy is dissipated to the bulk.

Here we consider the case of a correlated electronic system as described by a Hubbard chain with a finite interaction U. Time-dependent density-matrix renormalization-group calculations are performed to obtain the retarded spin susceptibility at the coupling site. This in turn determines the memory kernel of the classical integro-differential equation of motion for the spin dynamics, which is solved by standard propagation techniques.

In the metallic phase at quarter filling the susceptibility is characterized by two time scales corresponding to the two main electronic dissipation channels, namely (i) transport of excitations via correlated hopping and (ii) via excitations of correlation-induced magnetic moments. For strong U, these channels become active on largely different time scales, namely (i) on a short one given by the inverse band width and (ii) on a long scale given by the inverse magnetic coupling. This results in unconventional spin dynamics, e.g., in a nonmonotonic dependence of the relaxation time on U (see original publication).

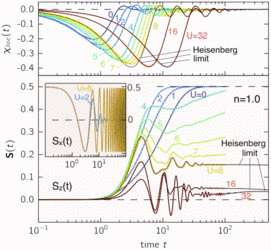
For a half-filled Hubbard model, however, the Mott gap blocks dissipation via correlated hopping, and for strong U the susceptibility is dominated by spin-flip processes only. These are fully covered by the emerging low-energy Heisenberg model (see the scaling behavior in Fig.1, top).

The necessity for dissipation via spin-only processes then leads to a striking new phenomenon (see Fig.1, bottom): With increasing U, the spin relaxation time first decreases as expected but for U larger than a critical value of about Uc=8, the relaxation time diverges, and there is a crossover to an incompletely relaxed, “stationary” state. The stationary state on an intermediate time scale originates when the bandwidth of magnetic excitations gets smaller than the field. On the time axis, the missing relaxation results from a strong memory effect: For memory times larger then 1/B the z-component of the torque on the spin averages to zero.

The incomplete spin relaxation can be understood as a transient “phase” similar to the concept of prethermalization which is known for purely electronic systems which, when parametrically close to an integrable point, do not thermalize directly but are trapped for some time in a prethermalized state. In our case, the “integrable point” is given by limit of infinite U, where the memory kernel is never active for any finite time t.

The situation is also reminiscent of quantum excitations that are metastable on an exponentially long time scale due to missing phase space for decay. A prominent example is a doublon which is metastable if the binding energy U largely exceeds the bandwidth and thus has to be dissipated in an unlikely high-order scattering process. In our case of classical spin degrees of freedom, one would expect that relaxation via dissipation of arbitrarily small amounts of energy is still possible. Our results show, however, that this is not the case.

Concluding, the real-time dynamics of correlated quantum-classical hybrid models are not well understood. The present study has shown that a merger of known classical and quantum concepts is highly interesting. Future work shall address questions like prethermalization, but also (non)integrability, eigenstate thermalization etc.

Download PDF

Roman Rausch, Hamburg University, Project B5