PD Dr. Elena Vedmedenko

The mean field theory or mean field approximation is one of the most famous and on the other hand one of the most underestimated theories in solid science.

Theories like Hartree-Fock, the Stoner model, and the RPA decoupling in the Green function theory base on the mean field approximation. Furthermore the Ginzburg-Landau theory is a mean field theory. The idea of the mean field theory is to replace the fluctuating fields coming from the inter- and intraparticle interactions by a nonfluctuating mean field.  As a consequence the mean field theory can be used to give a qualitative, however no quantitative description. Nevertheless, the mean field theory is exact in the limit of high dimensions (upper critical dimension) and in the case of strong long-range interactions.

For the classical Heisenberg model: 

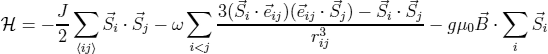
one has to replace the magnetic moment 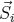 by 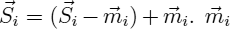 is the mean value of

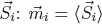. We get for : 

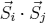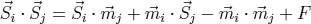
with the fluctuating term 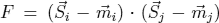.  In the mean field approximation we have to set  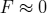. Furthermore, the last term  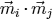can be skipped. This term only scales the zero energy. Therefore, we get for the mean field Hamiltonian: 

. 

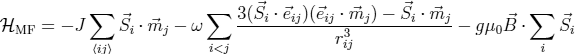The magnetization can be calculated with: 

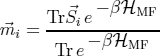where 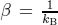. Within the calculation  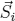 is given by spherical coordinates and the trace  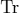 by the integration over the surface of an unit sphere: 

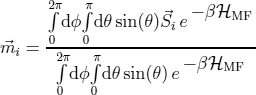
With this method we could show that near the Curie temperature 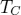 a deviation between the magnetization of a vortex core and the surrounding magnetization (domain) can be seen [1]. The vortex core magnetization shows a faster decrease than the magnetization of the domain. This means that additional to the thermal spin wave excitation and a superparamagnetic behavior of the vortex core longitudinal fluctuations near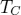  

play a role. Fig. 1 shows the magnetization of vortex core and domain: Two different critical temperatures can be seen. The explanation is simple: Due to the reduced exchange and dipole-dipole interaction in the vortex core stronger fluctuations can be investigated leading to to a rapidly decrease of the magnetization. Within the mean field approximation the fluctuations are neglected, however the effect can be clearly seen. This mean that one can assume that the mean field theory underestimates this effect and reality a stronger deviation will be found.   

Furthermore, we have used the mean field approximation in our recent concerning the spin-spin correlation in ferromagnetic nanostructures [2]. However, it has been shown that the mean field theory fails in this case. The cause are the missing fluctuations. 

Fig.: Magnetization over temperature of a magnetic vortex: core = magnetization of the vortex core and domain = magnetization of the surrounding magnewtic moments. 

-----------------

[1] R. Wieser, U. Nowak und K. D. Usadel, Thermodynamic behavior of nanomagnets with a vortex configuration, Phys. Rev. B 74, 094410 (2006).

[2] E. Y. Vedmedenko, N. Mikuszeit, T. Stapelfeldt, R. Wieser, M. Potthoff, A. I. Lichtenstein und R. Wiesendanger, Spin-spin correlations in ferromagnetic nanosystems, Eur. Phys. J. B. 80, 331 (2011)

A Monte Carlo simulation is a stochastic method, which relies on repeated random experiments. This method is mainly used, if it is impossible or infeasible to compute an exact result. The calculated observables are statistical averages, whose variance strongly depends on the number of performed random samplings.

We use Monte Carlo simulations to model and predict the physical properties of our sample systems. Here, the energy and the spatially resolved magnetization of the simulated system are the for us most important observables. In a Monte Carlo simulation random states are created according to a predefined probability distribution. Depending on the problem, a suitable probability function has to be chosen, because it determines the trajectory the system traverse in phase space. An important characteristic of this method is, that the newly created states do not depend on the previous states, hence, the system does not have a memory. The repeated sampling of such states is called a Markov chain. By creating a Markov chain the discrete Monte Carlo algorithm satisfies the condition of detailed balance, which ensures, the system to relax into the canonical equilibrium. As in our group many different experiments are available, we can directly compare the results from simulations with real system. This combination between experimental and theoretical approaches allows further insight to the physical properties of the system under investigation. For further information and mathematical background of Monte Carlo simulations we refer to the literature [1]. 

Application

To increase the density of future magnetic storage devices the size of the magnetic bits, the carrier of the magnetic information, need to be decreased constantly. In our group we do not concentrate on the technical realization to shrink those bits, but to find the physical limits and to determine the technical limits, where the bit can still be controlled. The smaller the bit, the easier a bit is excited thermally. Hence, the smaller the bit, the smaller the temperature at which the magnetic information is lost. This phenomena is called superparamagnetism and is one of the biggest challenges for future storage technology. To define and understand the limits of superparamagnetism, we study the temperature region of the magnetic stability in dependence of the bit size [2], see figure 1. From Monte Carlo simulation we not only gain insight to the temperature dependent switching frequency, but also insight to the switching mechanism. By comparison between experiment and simulation, we could show, that even very small bits, consisting of less than 100 atoms, switch via nucleation and propagation of domain walls and not as assumed by coherent rotation [3]. 

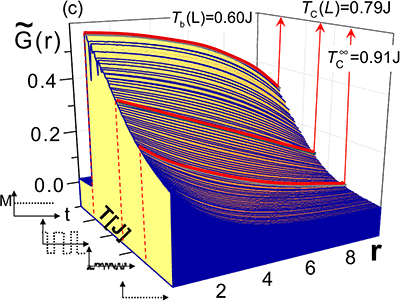
Figure 1: By fitting the correlation function G(r), one can determine the critical temperatures. 

In another study we propose a theoretical concept of domain wall manipulation by means of the tip of a spin-polarized scanning tunneling microscope and check our concept performing Monte Carlo simulations .The domain wall is driven by a spin-polarized current induced by the magnetic tip placed above the magnetic nanowire and then moved along its long axis with a current flowing through the vacuum barrier. The angular momentum coming from the spin-polarized current exerts a torque on the magnetic moments underneath the tip and leads to a displacement of the domain wall. By analyzing time-dependent Monte Carlo configurations , we can study the kinematics of the domain wall motion. Hence, we can observe how the systems relaxes into thermal equilibrium [4, Spin dynamic simulation]. Figure 2 shows an animation of a successful domain wall manipulation.

Figure 2: Animation of a successful domain wall manipulation. 

------------------

[1] D. P. Landau and K. Binder, A Guide to Monte-Carlo Simulations in Statistical Physics, Cambridge University Press, 2009

[2] E. Y. Vedmedenko, N. Mikuszeit, T. Stapelfeldt et al., Spin-spincorrelations in ferromagnetic nanosystems, European Physical Journal B 80, 331-336 (2011).

[3] S. Krause, G. Herzog, T. Stapelfeldt et al., Magnetization Reversal of Nanoscale Islands: How Size and Shape Affect the Arrhenius Prefactor, Physical Review Letters 103, 127202 (2009).

[4] T. Stapelfeldt, R. Wieser, E. Y. Vedmedenko et al., Domain WallManipulation with a Magnetic Tip, Physical Review Letters 107, 027203 (2011).